Vocabolario e Definizioni¶

Definiamo cosa è un grafo e quali sono le sue componenti.

Vertice

Un vertice (o nodo, in inglese “node” o “vertex”) è una parte fondamentale di un grafo. Può avere un nome, che chiameremo “chiave”. Può avere anche altre informazioni in più, chiamate “payload.”

Arco

Un arco (in inglese “arc” o “edge”) è un’altra parte fondamentale di un grafo. Un arco connette due vertici per mostrare che c’è una relazione tra di essi. Gli archi possono avere una direzione (essere “a senso unico”) oppure no. Nel primo caso parliamo di grafi diretti (in inglese digraph).

Peso

Gli archi possono essere pesati per mostrare che c’è un costo per andare da un vertice all’altro. Per esempio in un grafo di strade che connette una città a un’altra, il peso dell’arco potrebbe rappresentare la distanza tra due città.

Possiamo definire formalmente un grafo come segue: un grafo può essere rappresentato come \(G\) dove \(G =(V,E)\). Per il grafo \(G\), \(V\) è un insieme di vertici e \(E\) è un insieme di archi. Ogni arco è una tupla \((v,w)\) dove \(w,v \in V\). Possiamo aggiungere una terza componente alla tupla dell’arco per rappresentare il peso. Un sottografo \(S\) è un insieme di archi \(E'\) e vertici \(V'\) tali che \(E' \subset E\) e \(V' \subset V\). Un sottografo indotto di \(G\), \(G[V']\), con \(V' \subseteq V\), ha come vertici \(V'\) e come archi \(E'=\{(u,v)\in E, u,v\in V'\}\).

Figura  1 mostra un altro esempio di un grafo semplice pesato diretto. L’insieme dei vertici è:

e l’insieme degli archi è:

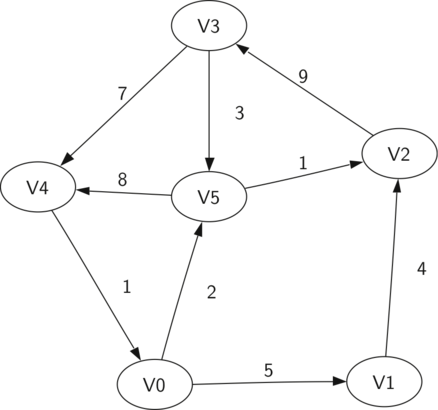
Figura 1: Un semplice esempio di grafo diretto

Il grafo di esempio in Figura 1 aiuta a illustrare altri due concetti fondamentali:

Cammino

Un cammino in un grafo è una sequenza di vertici che sono connessi da archi. Formalmente definiamo un cammino come \(w_1, w_2, ..., w_n\) tale che \((w_i, w_{i+1}) \in E\) con \(1 \le i \le n-1\). La lunghezza del cammino è il numero di archi che appartengono al cammino, ovvero \(n-1\). Il peso del cammino è la somma dei pesi di tutti gli archi nel cammino. Per esempio in Figura 1 il cammino da \(V3\) a \(V1\) è la sequenza di vertici \((V3,V4,V0,V1)\). Gli archi sono \(\left\{(v3,v4,7),(v4,v0,1),(v0,v1,5) \right\}\).

Ciclo

Un ciclo in un grafo diretto è un cammino che comincia e finisce nelle stesso vertice. Per esempio, in Figura 1 il cammino \((V5,V2,V3,V5)\) è un ciclo. Un grafo con nessuno ciclo è chiamato grafo aciclico. Un grafo diretto senza cicli è chiamato grafo diretto aciclico o DAG. Possiamo risolvere tanti problemi importanti se sappiamo che il problema può essere rappresentato come DAG.