Il problema dello scheduling degli intervalli¶

Il problema dello scheduling degli intervalli classico¶

Si consideri di avere un’unica risorsa - ad esempio un computer, o una stampante, o una lavatrice - condivisa da più persone, le quali hanno necessità di utilizzarla per svolgere delle attività in determinati intervalli temporali. Si assuma che la risorsa non possa essere utilizzata contemporaneamente da più persone. L’obiettivo è quello di massimizzare il numero di attività eseguibili sfruttando l’unica risorsa a disposizione. La soluzione ottima è quindi data dal sottoinsieme di attività compatibili di dimensione massima; nell’esempio precedente, {A, B} e {A, C} erano entrambe soluzioni ottime.

Soluzioni¶

Brute force

Un possibile approccio di risoluzione del problema classico dello scheduling degli intervalli è quello di “forza bruta”. In questo contesto, la soluzione di forza bruta si ottiene valutando, tra tutti i possibili sottoinsiemi di attività, quali sono quelli che contengono attività compatibili e, tra questi, scegliendone uno di dimensione massima. Sfortunatamente però questo algoritmo di risoluzione ha complessità esponenziale, e perciò non consente sempre di giungere alla soluzione in un tempo ragionevole.

Greedy

Fortunatamente, per quanto riguarda il problema dello scheduling degli intervalli classico, è noto anche un approccio di risoluzione maggiormente efficiente, basato sull’utilizzo di un algoritmo “greedy”. Un algoritmo greedy consente di giungere alla soluzione del problema facendo piccoli passi successivi e prendendo, a ciascun passo, una decisione in maniera miope, ovvero facendo una scelta che in quel momento sembra ottimale senza preoccuparsi delle evoluzioni future e senza mai tornare indietro sulle scelte fatte ai passi precedenti.

In questo contesto, un algoritmo di risoluzione greedy consiste in:

1. scegliere una regola semplice in base alla quale selezionare le attività da programmare,
2. selezionare l’attività da programmare,
3. eliminare dal set di attività programmabili tutte le attività incompatibili con essa,
4. ripetere i passi 2 e 3 fino a quando non ci sono più attività programmabili.

Dunque, il punto cruciale nella progettazione di un algoritmo di questo tipo è la scelta della regola sulla base della quale effettuare la selezione; infatti, ci sono diverse regole che potrebbero apparire “naturali” ma che purtroppo non consentono di ottenere il risultato desiderato.

Una di queste è la regola secondo cui, ad ogni passo, occorre sempre selezionare l’attività che inizia prima tra quelle disponibili, ovvero quella che ha \(s_{i}\) minimo; ciò appare sensato in quanto in questo modo si inizia ad usare la risorsa prima possibile. Sfortunatamente però, questa regola non consente sempre di ottenere la soluzione ottima; ad esempio, può accadere che l’attività che inizia prima tra quelle disponibili sia molto lunga e incompatibile con molte altre, come è possibile osservare in Figura 1.

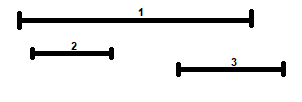
Figura 1: Esempio in cui selezionare sempre l’attività che inizia prima tra quelle disponibili non dà luogo alla soluzione ottima.

Un’altra regola che potrebbe apparire sensato adottare è quella di selezionare sempre l’attività che ha durata minore tra quelle disponibili, ovvero quella che ha \(f_{i} - s_{i}\) minimo; ciò nell’ottica di selezionare, ove possibile, tante attività brevi, che si pensa possano essere più spesso compatibili con altre attività rispetto ad attività più lunghe. Sfortunatamente però nemmeno questa regola, come è evidente in Figura 2, consente sempre di ottenere la soluzione ottima.

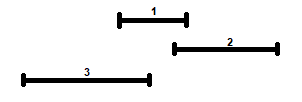
Figura 2: Esempio in cui selezionare sempre l’attività più breve tra quelle disponibili non dà luogo alla soluzione ottima.

Un’alternativa potrebbe essere quella di selezionare sempre l’attività che ha meno conflitti, ovvero quella che presenta il minor numero di attività incompatibili. Nemmeno questa regola di selezione però consente sempre di arrivare alla soluzione ottima, come è evidente in Figura 3.

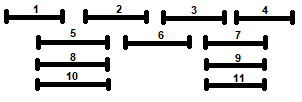
Figura 3: Esempio in cui selezionare sempre l’attività che ha il minor numero di conflitti tra quelle disponibili non dà luogo alla soluzione ottima.

Infine, un’ulteriore possibile regola potrebbe essere quella di selezionare sempre l’attività che finisce prima, ovvero quella che ha \(f_{i}\) minimo; anche quest’idea appare piuttosto naturale, in quanto prevede lo svolgimento dell’attività che consente di liberare il prima possibile l’unica risorsa a disposizione per lo svolgimento di attività successive. E’ possibile dimostrare che questa regola di selezione è quella che dà sempre luogo alla soluzione ottima.

Implementazione della soluzione ottima¶

L’algoritmo di risoluzione ottimo è quindi il seguente:

procedure ends_first1(1, 2, ..., n):
    candidate = {1, 2, ..., n}
    soluzione = {}

    while candidate =! {} do
        k <- attività con tempo di fine minore tra le attività candidate
        soluzione <- soluzione U {k}
        candidate <- candidate - {k}
        rimuovere dalle candidate tutte le attività incompatibili con k
    end while

    return soluzione
end procedure

Inizializzazione dell’algoritmo:

• si hanno \(n\) attività da programmare (le attività candidate).
• si hanno 0 attività già programmate (la soluzione è vuota).

Componente iterativa dell’algoritmo: ad ogni passo, l’algoritmo seleziona l’attività che finisce prima, la aggiunge alla soluzione e al contempo la rimuove dalle attività candidate; inoltre, rimuove dall’insieme delle candidate anche tutte le attività incompatibili con quella selezionata. Questa procedura viene iterata fino a quando l’insieme delle attività candidate non rimane vuoto, e quindi non è possibile programmare ulteriori attività; a quel punto, l’algoritmo restituisce la soluzione ottima, ovvero un sottoinsieme di attività compatibili di dimensione massima.

Questo algoritmo, sebbene consenta in teoria di giungere alla soluzione ottima, non è efficiente; infatti richiede, ad ogni passo, di scorrere ripetutamente l’intero insieme delle attività candidate: prima per selezionare l’attività con minor tempo di fine, poi per eliminare tutte le attività incompatibili con quella selezionata. Vediamo ora come progettare un algoritmo maggiormente efficiente.

• Per evitare di dover scorrere, ad ogni passo dell’algoritmo, l’intero insieme delle candidate per selezionare l’attività che finisce prima, è sufficiente ordinare le attività candidate in maniera non decrescente in base al loro tempo di fine, una tantum, all’inizio dell’algoritmo. Ciò consente, ad ogni passo, di trovare l’attività che finisce prima -tra quelle non ancora considerate- scorrendo semplicemente in avanti di una posizione l’insieme delle candidate ordinato.

• Per evitare di dover scorrere, ad ogni passo dell’algoritmo, l’intero insieme delle candidate per rimuovere da esso le eventuali attività incompatibili con l’attività appena selezionata, un’opzione è semplicemente quella di lasciare questo insieme invariato. In questo modo però, esso potrà contenere anche attività incompatibili con attività precedentemente selezionate, che quindi non dovranno quindi essere aggiunte alla soluzione. Ciò rende necessaria l’introduzione di un controllo, ad ogni passo, sulla compatibilità o meno della candidata con le attività già selezionate; soltanto in caso di compatibilità infatti essa dovrà essere aggiunta alla soluzione. Per sapere se una candidata è compatibile con tutte le attività precedentemente selezionate, è sufficiente verificare che essa inizi dopo la fine dell’ultima attività aggiunta alla soluzione. Quest’ultima infatti, come conseguenza dell’ordinamento, sarà necessariamente quella con maggior tempo di fine tra le attività selezionate; perciò, se la candidata è compatibile con essa, è necessariamente compatibile anche con tutte quelle precedentemente selezionate.

  Dal punto di vista dell’implementazione, dato che nessuna attività viene rimossa dall’insieme delle candidate, non si avrà più un ciclo while che itera fino a quando l’insieme delle candidate non rimane vuoto, ma si avrà piuttosto un ciclo for sulle n candidate iniziali.

• Infine, dato che al primo passo dell’algoritmo l’attività con minor tempo di fine viene necessariamente selezionata, è possibile aggiungerla direttamente alla soluzione durante l’ inizializzazione dell’algoritmo ed in seguito effettuare un ciclo for soltanto sulle n-1 attività candidate rimanenti.

Una versione più efficiente dell’algoritmo di risoluzione precedentemente proposto è quindi la seguente:

procedure ends_first2(1, 2, ..., n):
    candidate <- ordina {1, 2, ..., n} per tempi di fine crescenti
    soluzione <- seleziona la prima candidata (ovvero l'attività che finisce prima)
    t <- seleziona il suo tempo di fine

    for activity <- 2 to n do                 # per tutte le attività candidate eccetto la prima (che è già stata selezionata)
        if s_{activity} >=  t then            # se l'attività candidata è compatibile con quelle già selezionate:
            soluzione <- soluzione U {activity} # 1) la aggiunge alla soluzione
            t <- f_{activity}                 # 2) aggiorna l'indicatore del tempo di fine delle attività selezionate
        end if
    end for

    return soluzione
end procedure

In questo algoritmo, t non è altro che una variabile in cui viene salvato il tempo di fine dell’ultima attività selezionata, che naturalmente viene aggiornata ogni volta che un’ulteriore attività viene aggiunta alla soluzione; essa viene utilizzata per verificare, ad ogni passo, la compatibilità o meno della nuova attività candidata con quelle precedentemente selezionate.

Supponiamo di utilizzare questo algoritmo per programmare 5 attività, i cui intervalli sono: (1, 3), (3, 6), (4, 6), (2, 5) e (7, 8).

procedure ends_first2((1, 3), (3, 6), (4, 6), (2, 5), (7, 8)):
    candidate <- {(1, 3), (2, 5), (3, 6), (4, 6), (7, 8)}
    soluzione <- {(1, 3)}
    t <- 3

    activity <- (2, 5)
        s_{activity} <  3 then do nothing

    activity <- (3, 6)
        s_{activity} ==  3 then
            soluzione <- {(1, 3), (3, 6)}
            t <- 6

    activity <- (4, 6)
        s_{activity} <  6 then do nothing

    activity <- (7, 8)
        s_{activity} > 6 then
            soluzione <- {(1, 3), (3, 6), (7, 8)}
            t <- 8

    return soluzione
end procedure

L’algoritmo restituisce quindi la seguente soluzione ottima: {(1, 3), (3, 6), (7, 8)}.

Occorre notare però che in questo caso la soluzione ottima a cui è possibile pervenire sfruttando l’algoritmo non è unica. Ciò si verifica perchè ci sono due attività candidate che hanno lo stesso tempo di fine: (3, 6) e (4, 6); ne consegue che gli intervalli considerati possono essere ordinati correttamente in base al loro tempo di fine sia come {(1, 3), (2, 5), (3, 6), (4, 6), (7, 8)}, sia come {(1, 3), (2, 5), (4, 6), (3, 6), (7, 8)}. Vediamo dunque quale soluzione produce l’algoritmo in quest’ultimo caso:

procedure ends_first2((1, 3), (3, 6), (4, 6), (2, 5), (7, 8)):
    candidate <- {(1, 3), (2, 5), (4, 6), (3, 6), (7, 8)}   # ordinamento alternativo
    soluzione <- {(1, 3)}
    t <- 3

    activity <- (2, 5)
        s_{activity} <  3 then do nothing

    activity <- (4, 6)
        s_{activity} >  3 then
            soluzione <- {(1, 3), (4, 6)}
            t <- 6

    activity <- (3, 6)
        s_{activity} <  6 then do nothing

    activity <- (7, 8)
        s_{activity} > 6 then
            soluzione <- {(1, 3), (4, 6), (7, 8)}
            t <- 8

    return soluzione
end procedure

L’algoritmo restituisce quindi la seguente soluzione alternativa, anch’essa ottima: {(1, 3), (4, 6), (7, 8)}.

Una traduzione dell’algoritmo in codice Python è la seguente:

def ends_first2(meetings):

    meetings = sorted(meetings, key=itemgetter(1))
    scheduling = [meetings[0]]
    t = meetings[0][1]

    for activity in range(len(meetings) - 1):

        if meetings[activity + 1][0] >= t:
            scheduling.append(meetings[activity + 1])
            t = meetings[activity + 1][1]

return scheduling

L’ argomento della funzione ends_first2 può essere:

1. Una lista (o una tupla) di liste, dove ogni lista annidata rappresenta l’intervallo temporale in cui un’attività deve essere svolta:

   arg_1 = [[1, 3], [2, 5], [3, 6]]
   arg_2 = ([1, 3], [2, 5], [3, 6])
   

2. Una lista (o una tupla) di tuple, dove ogni tupla annidata rappresenta l’intervallo temporale in cui un’attività deve essere svolta:

   arg_3 = [(1, 3), (2, 5), (3, 6)]
   arg_4 = ((1, 3), (2, 5), (3, 6))
   

La soluzione restituita dalla funzione invece sarà sempre una lista contenente gli intervalli selezionati sotto forma di liste (o di tuple) annidate, a seconda del formato in cui gli intervalli erano inizialmente rappresentati:

ends_first(arg_1) # restituisce: [[1, 3], [3, 6]]
ends_first(arg_2) # restituisce: [[1, 3], [3, 6]]
ends_first(arg_3) # restituisce: [(1, 3), (3, 6)]
ends_first(arg_4) # # restituisce: [(1, 3), (3, 6)]

Ciò si verifica perchè, ogni volta che si ispeziona l’intervallo di un’attività che si rivela essere compatibile con le attività selezionate fino a quel momento, lo si aggiunge alla lista contenente la soluzione tramite il metodo append. Di conseguenza, se questo intervallo era contenuto in una tupla, si avrà come soluzione una lista di tuple; se invece era contenuto in una lista, si avrà come soluzione una lista di liste.

All’interno dell’algoritmo gli intervalli devono essere ordinati in maniera non decrescente rispetto al loro tempo di fine. Il tempo di fine di ciascun intervallo si trova nella posizione 1 di ciascuna lista (o tupla) annidata; è dunque necessario accedervi per procedere all’ordinamento. Per farlo, si sfrutta l’argomento opzionale key della funzione sorted; tale argomento consente infatti di specificare una funzione che verrà utilizzata per estrarre, da ciascun elemento che si vuole ordinare, una “chiave” sulla base della quale effettuare il confronto. In questo caso, la funzione specificata tramite l’argomento key è itemgetter(), presente nel modulo operator; in particolare, key=itemgetter(1). itemgetter(1) consente di leggere gli elementi nella posizione 1 di ciascuna lista (o tupla) annidata, ovvero i tempi di fine di ciascun intervallo; in base ad essi, si procede poi all’effettuazione dell’ordinamento desiderato.

N.B: è possibile specificare l’argomento key anche all’interno del metodo sort; in particolare, utilizzando, al posto di meetings=sorted(meetings, key=itemgetter(1)), meetings.sort(key=itemgetter(1)) si ottiene lo stesso risultato. Anzi, il metodo sort è addirittura più efficiente in quanto non crea una nuova lista ordinata, ma agisce andando a modificare direttamente la lista che gli è stata passata (ecco perchè non è necessario effettuare una riassegnazione del risultato); al contrario, la funzione sorted crea una nuova lista ordinata (e rende dunque necessaria una riassegnazione del risultato). Si è preferito comunque utilizzare la funzione sorted poichè il metodo sort non è applicabile alle tuple, mentre si voleva che la funzione ends_first2 funzionasse sia con intervalli sotto forma di liste che di tuple per una questione di generalità.

Complessita’

Supponiamo di avere \(n\) attività da programmare. Innanzitutto, la complessità di meetings=sorted(meetings, key=itemgetter(1)) è \(O(nlog_{2}n)\) sia nel caso medio sia nel caso peggiore. Il tempo di esecuzione di scheduling=[meetings[0]] invece è costante, come quello di t=meetings[0][1]. Infine, la complessità del ciclo for è \(O(n)\), poichè tale ciclo ha \(n-1\) iterazioni e al suo interno tutte le operazioni effettuate hanno tempo costante (incluso l’utilizzo del metodo append).

Dunque, la complessità totale dell’algoritmo è \(O(nlog_{2}n) + O(n) = O(nlog_{2}n)\) sia nel caso medio che nel caso peggiore. Il termine \(nlog_{2}n\) cresce più velocemente di un termine lineare, ma più lentamente di un qualsiasi polinomio in \(n\) con esponente strettamente maggiore di 1; si conclude dunque che l’algoritmo è abbastanza efficiente.