Rappresentazione mediante lista di liste¶

In un albero rappresentato come una lista di liste, cominceremo con le liste e scriveremo poi una struttura dati ricorsiva che possiamo esaminare direttamente.

In un albero, memorizzeremo solo il valore della radice come primo elemento della lista. Il secondo elemento della lista sarà una lista che rappresenta il sottoalbero sinistro, mentre il terzo elemento della lista rappresenta il sottoalbero destro. Per illustrare questa strategia di memorizzazione, osserviamo l’esempio in Figura 1, che mostra un semplice albero e le lista corrispondenti.

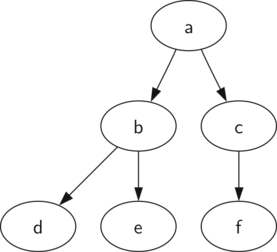
Figura 1: Un albero

myTree = ['a',   #root
      ['b',  #left subtree
       ['d' [], []],
       ['e' [], []] ],
      ['c',  #right subtree
       ['f' [], []],
       [] ]
     ]

Nota che possiamo accedere ai sottoalberi della lista usando l’indicizzazione standard delle liste. La radice dell’albero è myTree[0], il sottoalbero sinistro della radice è myTree[1], e il sottoalbero destro è myTree[2]. ActiveCode 1 illustra come creare un semplice albero usando una lista. Una volta che l’albero è stato costruito, possiamo accedere alla radice e ai sottoalberi. Una proprietà importante di questa lista di liste è che la struttura di una lista che rappresenta un sottoalbero rappresenta ancora un albero. Dunque, la struttura dati stessa è ricorsiva! Un sottoalbero che ha una radice e due liste vuote come sottoalberi è una foglia. Un’altra proprietà importante è che può essere generalizzata a un numero arbitrario di sottoalberi. In questo caso, l’albero non è binario e un altro sottoalbero è semplicemente un’altra lista oltre ai primi due.

Formalizziamo questa definizione della struttura dati, fornendo alcune funzioni che ci rendono l’uso delle liste più comodo. Nota che non definiamo una classe per gli alberi binari. Le funzioni ci aiutano semplicemente a manipolare le liste standard, pensandole alla luce del fatto che stiamo lavorando con alberi.

def BinaryTree(r):
    return [r, [], []]

La funzione BinaryTree costruisce semplicemente un albero che ha una radice e due liste vuote come sottoalberi. Per aggiungere un sottoalbero sinistro alla radice di un albero, abbiamo bisogno di inserire una nuova lista in seconda posizione della lista radice. Dobbiamo stare attenti. Se la lista ha già qualcosa in seconda posizione, abbiamo bisogno di tenerne traccia, e questo diventerà il sottoalbero sinistro della lista che stiamo aggiungendo. Listing 1 mostra il codice Python per inserire un figlio sinistro.

Listing 1

def insertLeft(root,newBranch):
    t = root.pop(1)
    if len(t) > 1:
        root.insert(1,[newBranch,t,[]])
    else:
        root.insert(1,[newBranch, [], []])
    return root

Per inserire un figlio sinistro, prima otteniamo una lista (eventualmente vuota) che corrisponde al figlio sinistro corrente. Aggiungiamo poi il nuovo figlio sinistro, mettendo il vecchio figlio sinistro come figlio sinistro di quello nuovo. Questo permette di inserire un nuovo nodo nell’albero in qualsiasi posizione. Il codice per insertRight è simile a insertLeft ed è mostrato in Listing 2.

Listing 2

def insertRight(root,newBranch):
    t = root.pop(2)
    if len(t) > 1:
        root.insert(2,[newBranch,[],t])
    else:
        root.insert(2,[newBranch,[],[]])
    return root

Per completare, come mostrato in Listing 3, scriviamo una coppia di funzioni di accesso per avere o impostare il valore della radice o quello dei sottoalberi sinistro e destro.

Listing 3

def getRootVal(root):
    return root[0]

def setRootVal(root,newVal):
    root[0] = newVal

def getLeftChild(root):
    return root[1]

def getRightChild(root):
    return root[2]

ActiveCode 2 usa le funzioni che abbiamo appena scritto. Lasciamo come esercizio quello di disegnare l’albero risultante da questo insieme di chiamate.