Visite di Alberi¶

Adesso che abbiamo esaminato le funzionalità di base della nostra struttura dati, è tempo di dare uno sguardo al loro comune uso. Le forme con cui un albero può essere interrogato possono essere divise in tre. La differenza è l’ordine con cui i nodi sono visitati. Chiamiamo questa visita dei nodi “attraversamento”. Le tre visite che vedremo sono chiamate: anticipata, simmetrica, posticipata (in inglese, rispettivamente, preorder, inorder e postorder). Cominciamo col definirle vedendo alcuni esempi in cui possono essere utili.

anticipata

In una visita anticipata, visitiamo prima la radice, poi ricorsivamente facciamo una visita anticipata del sottoalbero sinistro seguita da una visita anticipata del sottoalbero destro.

simmetrica

In una visita simmetrica, facciamo una visita simmetrica del sottoalbero sinistro, visitiamo la radice, e infine facciamo una visita simmetrica del sottoalbero destro.

posticipata

In una visita posticipata, facciamo ricorsivamente una visita posticipata del sottoalbero sinistro e del sottoalbero destro seguita da una visita del nodo radice.

Vediamo alcuni esempi che illustrano ciascuna delle tre visite all’opera. Prima vediamo la visita anticipata. Come esempio di albero da attraversare, rappresenteremo il libro originale (da cui è tratta questa traduzione) come un albero. Il libro è la radice dell’albero e ogni capitolo è un figlio della radice. Ogni sezione di un capitolo è un figlio del capitolo e ogni sottosezione è un figlio della sezione, e così via. Figura 5 mostra una versione limitata del libro con solamente due capitoli. Notiamo che l’algoritmo di attraversamento funziona con alberi con un numero qualsiasi di figli, ma considereremo solo alberi binari per adesso.

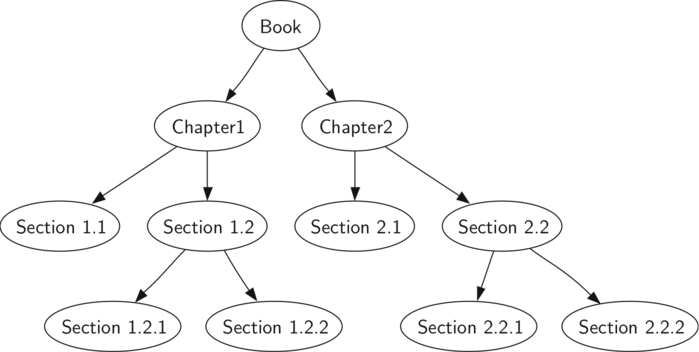
Figura 5: Rappresentazione di un libro come albero

Supponiamo di voler leggere questo libro dall’inizio alla fine. La visita anticipata ci fornisce esattamente questo ordine. Partendo dalla radice (il nodo Book) useremo le istruzioni date dalla visita anticipata. Richiamiamo ricorsivamente preorder sul figlio sinistro, in questo caso Chapter1. Chiamiamo ancora ricorsivamente preorder sul figlio sinistro per ottenere la Section 1.1. Dal momento che Section 1.1 non ha figli, non facciamo ulteriori visite ricorsive. Quando abbiamo finito con Section 1.1, ci muoviamo al livello superiore dell’albero verso Chapter 1. A questo punto abbiamo ancora bisogno di visitare il sottoalbero destro di Chapter 1, che è Section 1.2. Come prima visitiamo il sottoalbero sinisto, che ci porta a Section 1.2.1, poi visitiamo il nodo Section 1.2.2. Finita Section 1.2, ritorniamo verso Chapter 1. A questo punto ritorniamo al nodo Book e seguiamo la stessa procedura per Chapter 2.

Il codice per scrivere visite di alberi è sorprendentemente elegante, perché le visite sono scritte ricorsivamente. Listing 2 mostra il codice Python per una visita anticipata di un albero binario.

Listing 2 mostra una versione di visita anticipata scritta come funzione esterna che prende un albero binario come parametro. Il nostro caso base semplicemente controlla se l’albero esiste. Se il parametro tree è None, allora la funzione ritorna senza far nulla.

Listing 2

def preorder(tree):
    if tree:
        print(tree.getRootVal())
        preorder(tree.getLeftChild())
        preorder(tree.getRightChild())

L’algoritmo per la visita postorder, mostrato in Listing 3, è molto simile a preorder eccetto per il fatto che la stampa è spostata alla fine della funzione.

Listing 3

def postorder(tree):
    if tree != None:
        postorder(tree.getLeftChild())
        postorder(tree.getRightChild())
        print(tree.getRootVal())

Un uso comune per le visite posticipate è la valutazione di un albero di parsing. E’ possibile infatti immaginare una espressione aritmetica come un albero in cui l’operatore aritmetico, per esempio +, sta nella radice e combina il risultato ottenuto dalla parte sinistra del + e il risultato ottenuto dalla parte destra. Quello che stiamo facendo è valutare il sottoalbero sinistro, valutare il sottoalbero destro e combinare i due risultati nella radice attraverso l’operatore. Assumiano che il nostro albero binario memorizzi solamente espressioni. Riscriviamo la funzione di valutazione, modellandola come la visita postorder in Listing 3 (vedi Listing 5).

Listing 5

def postordereval(tree):
    opers = {'+':operator.add, '-':operator.sub, '*':operator.mul, '/':operator.truediv}
    res1 = None
    res2 = None
    if tree:
        res1 = postordereval(tree.getLeftChild())
        res2 = postordereval(tree.getRightChild())
        if res1 and res2:
            return opers[tree.getRootVal()](res1,res2)
        else:
            return tree.getRootVal()

Notiamo che la forma in Listing 3 è la stessa di quella in Listing 5, eccetto che invece di stampare la chiave alla fine della funzione, la ritorniamo. Questo permette di salvare i valori ritornati dalle chiamate ricorsive alle linee 6 e 7. Usiamo allora i valori salvati con l’operatore alla riga 9.

Infine, l’ultima visita che vediamo è la visita simmetrica. Nella visita simmetrica, visitiamo il sottoalbero sinistro, seguito dalla radice e infine dal sottoalbero destro. Listing 6 mostra il nostro codice. Notiamo che tutte e tre le funzioni di visita differiscono per la posizione in cui l’istruzione print appare rispetto alle due funzioni ricorsive.

Listing 6

def inorder(tree):
  if tree != None:
      inorder(tree.getLeftChild())
      print(tree.getRootVal())
      inorder(tree.getRightChild())

Se facciamo una semplice visita simmetrica di un albero di parsing, quello delle espressioni aritmetiche che abbiamo visto prima, otteniamo l’espressione originale, senza le parentesi. Modifichiamo il codice in modo da mettere anche le parentesi nell’espressione. Le sole modifiche che dobbiamo fare rispetto al codice originale sono le seguenti: stampa una parentesi aperta prima della chiamata ricorsiva al sottoalbero sinistro, stampa una parentesi chiusa dopo la chiamata ricorsiva al sottoalbero destro. Il codice modificato è mostrato in Listing 7.

Listing 7

def printexp(tree):
  sVal = ""
  if tree:
      sVal = '(' + printexp(tree.getLeftChild())
      sVal = sVal + str(tree.getRootVal())
      sVal = sVal + printexp(tree.getRightChild())+')'
  return sVal

Notiamo che la funzione printexp come l’abbiamo implementata mette parentesi intorno a ogni numero. Sebbene non sbagliato, queste parentesi non sono necessarie. Lasciamo come esercizio modificare la funzione printexp in modo da rimuovere queste parentesi superflue.