Vocabolario e Definizioni¶
Definiamo formalmente un albero e le sue componenti.
- Nodo
- Un nodo è una parte fondamentale di un albero. Può avere un nome, che chiamiamo chiave, “key.” Un nodo può contenere ulteriori informazioni, chiamate “payload.”
- Arco
- Un arco è un’altra parte fondamentale di un albero. Un arco connette due nodi per mostrare che c’è una relazione tra di loro. Ogni nodo eccetto la radice è connesso con esattamente un arco entrante. Ogni nodo può avere diversi archi uscenti.
- Radice
- La radice di un albero è il solo nodo nell’albero che non ha archi entranti. In Figura 2, / è la radice dell’albero.
- Cammino
- Un cammino è una lista ordinata di nodi che sono connesse da archi. Per esempio, Mammal \(\rightarrow\) Carnivora \(\rightarrow\) Felidae \(\rightarrow\) Felis \(\rightarrow\) Domestica è un cammino.
- Figli
- L’insieme dei nodi \(C\) che hanno archi entranti dallo stesso nodo sono detti figli dello stesso nodo. In Figura 2, i nodi log/, spool/, and yp/ sono figli del nodo var/.
- Genitore
- Un nodo è il genitore di tutti i nodi a cui è connesso con archi uscenti. In Figura 2 il nodo var/ è il genitore dei nodi log/, spool/, and yp/.
- Fratelli
- Nodi che sono figli dello stesso genitore sono detti fratelli. I nodi etc/ e usr/ sono fratelli nell’albero del filesystem.
- Sottoalbero
- Un sottoalbero è un insieme di nodi e archi tali che i nodi \(S\) comprendono un genitore e tutti i suoi discendenti e gli archi sono tutti gli archi dell’albero che hanno entrambi gli estremi in \(S\).
- Nodo Foglia
- Una foglia è un nodo senza figli. Per esempio, Human e Chimpanzee sono nodi foglia in Figura 1.
- Livello
- Il livello di un nodo \(v\) è il numero di archi sul cammino dal nodo radice a \(v\). Per esempio, il livello del nodo Felis in Figura 1 è cinque. Per definizione, il livello della radice è zero.
- Altezza
- L’altezza di un albero è uguale al livello massimo di qualsiasi nodo nell’albero. L’‘albero dell’albero in Figura 2 è due.
Possiamo adesso dare una definizione formale di albero. Daremo due definizioni. La prima coinvolge archi e nodi. La seconda, molto utile, è una definizione ricorsiva..
Definizione Uno: Un albero consiste di un insieme di nodi e archi che connette coppie di nodi. Un albero ha le seguenti proprietà.
- Un nodo dell’albero è chiamato radice.
- Ogni nodo \(v\), eccetto la radice, è connesso da un arco esattamente a un altro nodo \(p\), dove \(p\) è il genitore di \(v\).
- C’è un solo cammino dalla radice a ogni nodo.
Se ogni nodo nell’albero ha al massimo due figli, parliamo di albero binario.
Figura 3 mostra un albero che rispetta la Definizione Uno. Le punte degli archi indicano la direzione della connessione.
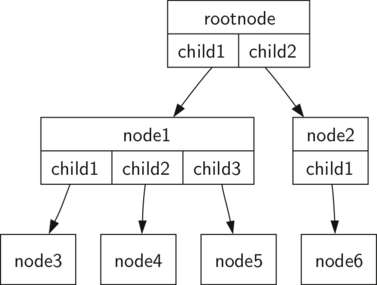
Figura 3: Un albero che consiste di un insieme di nodi e archi
Definizione Due: Un albero è vuoto o consiste di una radice e zero o più sottoalberi, ciascuno dei quali è ancora un albero. La radice di ciascun sottoalbero è connessa alla radice dell’albero genitore da un arco.
Figura 4 mostra la definizione ricorsiva di un albero. Usando la definizione ricorsiva di un albero, sappiamo che l’albero in Figura 4 ha almeno quattro nodi, dal momento che ciascuno dei triangoli rappresenta un sottoalbero che contiene almeno una radice. Potrebbe contenere molti altri nodi, ma non lo sappiamo a meno che non andiamo più in profondità all’interno di essi.
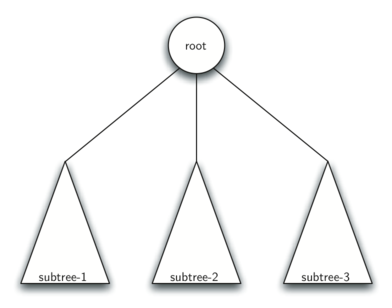
Figura 4: Definizione ricorsiva di albero